The weighted mean of a discrete set of numbers 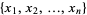 with weights
with weights 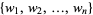 is given by
is given by
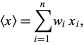 |
(1)
|
where each weight 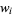 is a nonnegative real number and
is a nonnegative real number and
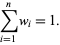 |
(2)
|
For a continuous set of numbers 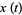 parameterized
by the variable
parameterized
by the variable 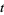 defined over the set
defined over the set 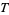 and a
and a
weight distribution
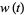 also defined over
also defined over 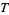 with
with 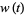 nonnegative
for all
nonnegative
for all 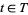 and
and
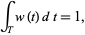 |
(3)
|
the weighted mean of  is given by
is given by
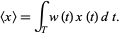 |
(4)
|
Weighted means have many applications in physics, including finding the
center of mass and moments of inertia of an object with a known density
distribution and computing and electric and magnetic multipole moments
of charge and current distributions, respectively.
Weighted means are also commonly used in statistics, for instance, in population studies.
from : http://mathworld.wolfram.com/WeightedMean.html
====================================================================
가중평균 [加重平均, weighted average]
N개의 수치의 평균값을 구할 때 중요도나 영향도에 해당하는 각각의 가중치를 곱하여 구한 평균값이다.
이를테면, N개의 수치 x1,x2,…,xn의 산술평균 M은,
M=(x1+x2+…+xn)/N
으로 구할 수 있다. 그런데 이 N개 중에 x1이 f1개, x2가 f2개, …, xn이 fn개 있다고 하면,
f1+f2+…+fn=N
이 되고, 이 N개의 수치의 합계는,
f1x1+f2x2+…+fnxn
이 되므로 M의 식은
M=(f1x1 + f2x2+…+fnxn)/N
이 된다. 이것을 서로 다른 n개의 수치 x1,x2…,xn에 각각 f1f2…,fn이라는 가중치가 붙었다고 생각하여, M의 식을 가중평균이라 한다. 이것은 수치 x1,x2,…,xn의 중요도나 영향도가 각각 f1f2…,fn만큼있다고 생각해도 좋다. 이를테면, 발표에 나타낸 A, B, C 3지역의 평균 사망률을 산출하면,
(2.5×400
+ 1.8×1000 + 2.0×600)/(400+1000+600) = 2.0
으로 계산할 수 있다. 이것은 인구를 웨이트로 하여 가중평균한 것이다.
from : http://100.naver.com/100.nhn?docid=2213